Integer Poetry: Chapter 1
Adding (Haiku)
Adding Integers
You can use I have, I owe
You can think money.
Subtracting (Tanka)
This cannot be done
always use the opposite
use pictures to help
negative to positive
Algebra tiles work too
Quotative Division (Haiku)
How many groups of
show using pictures and squares
find out the answer
Partitive Division (Tanka)
Sharing equally
one for me and one for you
Is expressed in different ways
multiplicative inverse
answer by pictures
Pratt's Integer Law (Free Verse)
When using the rule its not
all that tough, all you need to do is
to know your stuff. When there is an
even amount of negative integers it equals
positive as you can see, while when there is
an odd amount of negatives it equals negative, silly!
So use the rule when it comes to tests and then
you'll see who's the best!
Chapter 2- Combine like terms and The distributive Property
Script:
Script:
Peter: Hey bob what are you doing?
Bob:I'm just doing some algebra homework I got from school, and they seem very tough.
Peter:Would you like some help?
Bob:Sure I would like some help from you!
Bob:Okay the first one is n plus 3 subtract 5n plus 12 and I think the answer is negative 6n plus 15.
Peter:Well Bob that's the wrong answer because you didn't combine like terms, firstly find things that are the same like variable with the same variable, its like you add the n with another n which is n subtract 5n which gives you negative four n then you do the same thing with the integers, positive 3 plus positive 12 which equals positive 15 so the answer is really negative 4n plus 15.
Bob:Oh, so that's how you combine like terms.
Peter:Yes, now about the other question that you were trying to explain?
Bob:Oh yes, the other one it says 2+4 then in the bracket it says 3n+8. How do you do that? Plus I answered 12n+10.
Peter:Well what you just said was the Distributive Property. The answer you just said was wrong. Firstly to answer the question look for a number beside the bracket, that means that you are multiplying. So 4 times 3n equals 12n then you multiply 4 times 8 which equals 32. After that you take 2+ from earlier and add it with the others. So that means 2+12n+32equals 12n+34. 12n+34 is the real answer.
Bob:Oh so that's how you do distributive property. Thanks Peter for helping me with my homework now I understand Combining like terms and Distributive property.
Peter:Your welcome Bob!
Chapter 3 One Step Solving Equation
Additive Type:

Subtractive Type:
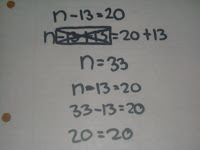
Multiplicative Type:

D type:


I absolutely loved "Pratt's Integer Law". Very cool. All the poetry is wonderful! I will send my students to this page!
from Ontario Canada.
December 4, 2008 at 8:46 PM
I absolutely love your math poetry! I can't wait to show your work to the 4th and 5th grade math teachers where I work (Jacksonville, FL) so they can try something similar with their students. Great job!
December 4, 2008 at 8:46 PM
Thanks for the great poetry. I like the subraction one the best. Mrs. Royer, from west central Iowa.
December 4, 2008 at 9:08 PM
AWESOME JOB JAY ! Nice use in colours and you have great rhyming skills (:
December 4, 2008 at 9:13 PM
Hey John Ray , Good job . I liked the colors and i liked how it ryhmed.
December 5, 2008 at 9:16 PM
Nice job Jay, but when i was reading your tanka I think you made some syllable mistakes but i really liked it. And I also liked your free verse on Pratt's Integer law nicely done. Keep up the good work!!
December 5, 2008 at 9:24 PM
JAY ! Good job on your poems ! There well done ! Good choice on the colours, your poems are easy to read. Either than that keep up the good work !
Oh and btw, Gian, this isn't John Rays work, haha its JAYS ! (:
December 7, 2008 at 7:29 PM