R.A.T means Right Angle Triangle!
The right triangle has a 90 degree angle. The red square on the triangle shows where
the 90 degree angle is.The green symbol in the top corner of the triangle is called the Theta.
The grey symbol in the bottom corner of the triangle is called the Beta.
Together, the two angles (the Theta and the Beta) equal 90 degrees, they are complimentary.
The longest side of the triangle, the hypotenuse, is ALWAYS labeled as C.
The two other sides are labeled A and B (Note: it doesn't matter which side they go on!!! Although, an easy way to remember is A for Altitude (going up) and b for bottom, which is pretty self explanatory!) Together, side A and B make up the 90 degree angle. They are also called the legs of the triangle.
(the colours of the things in or around the triangle go with the colours of the words)
Pythagoras
Pythagoras was the person who proved the Pythagorean Theorem.
Pythagoras was the person who proved the Pythagorean Theorem. He was born in Greece, and was one of the first important math people.
No one really knows weather he did exist or not.
He really liked math and music.
He was a teacher, and a philosopher.
He was the one who figured out that the Earth is a sphere, the circumference of the Earth, and that the world revolved around the sun.
He was also the first vegan, he said he could hear his friends voice from a dog.
THE PYTHAGOREAN THEOREM
Pythagoras is famouse for proving the theorem.
Side a is the smallest, b the middle sized, and c the biggest.
You show this by taking b, and putting it into c, and then you cut a into certain sized pieces, and that proves that a² + b² = c².
Square.
A square has 4 right angles.
The internal angle is 360 degrees.
If you cut the square from one corner to the opposite corner, you'll have two triangles.
The single black lines on each side of the square tell you that all the sides are the same, they are lines of symmetry (indicating that this shape is a square and not a rectangle.)
A square has 4 right angles.
The internal angle is 360 degrees.
If you cut the square from one corner to the opposite corner, you'll have two triangles.
The single black lines on each side of the square tell you that all the sides are the same, they are lines of symmetry (indicating that this shape is a square and not a rectangle.)
Each side of the square is the same length.
Problem 1.
So at first, all I knew was that b is 8mm and c is 10mm.
And now, we have a, which is 6mm. But, there are two triangles, and side a on each is 6mm, which makes side a 12mm.
Problem 2.
A checkerboard is made of 64 small squares that each have a dimension of 3 cm X 3cm. The 64 small squares are arranged in eight rows of eight.
A. What is the length of the diagonal of a small square? Give your answer to the nearest tenth of a centimetre.
The length of the diagonal of a small square is 4.2cm.
Let C = length
a²+b²=c²
3²+3²=c²
9+9=c²
√18=√c²
4.2= c
B. What is the length of the diagonal of the board? Give your answer to the nearest centimetre.
B. What is the length of the diagonal of the board? Give your answer to the nearest centimetre.
The length of the diagonal of the board is 11cm Let C = length
a²+b²=c²
8²+8²=c²
(8x8) + (8x8) = c²
64+64=c²
√128 = c
11 = c
Video 1.
Video 2.
Video 2.
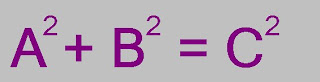
0 comments:
Post a Comment